首页>
科学探索>
最有趣数学：毕达哥拉斯树，勾股定理画出的一棵树

最有趣数学：毕达哥拉斯树，勾股定理画出的一棵树

2025-02-24 20:33:22阅读量：9 字体：大中小

导语：毕达哥拉斯树是由毕达哥拉斯利用勾股定理画出的一个无限重复图形，因为整体图形的形状像一棵树，所以也被称为“勾股树”，但是由于重叠限制，现实中的毕达哥拉斯树的面积是有限的6乘4，下面就跟着彩霞奇闻小编一起来看看吧!

毕达哥拉斯树是什么?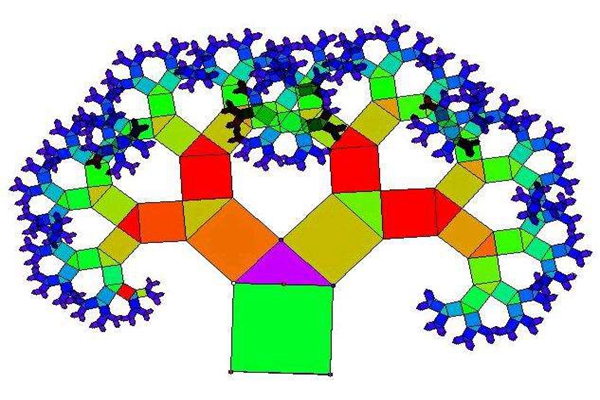

虽说数学是十分枯燥的，但是科学家总能从中找到无限的乐趣，毕达哥拉斯树就是由古希腊数学家毕达哥拉斯，利用勾股定理所画出的一个无限重复图形，当重复的次数够多时，就会形成一个树的形状，所以也有人称之为“勾股树”。

直角三角形和它的三条边延伸出的三个正方形，都具备着一些神奇的特征，比如直角三角形的面积小于等于大正方形面积的1/4，大于等于小正方形的1/2，而且两个小正方形等于大正方形的面积，同一次的所有小正方形面积和等于最大的正方形面积。

毕达哥拉斯树的简单画法

众所周知勾股定理就是直角三角形的两个直角边的平方和，等于斜边的平方，毕达哥拉斯利用这一点，在初始的大正方形上，做出了两个全等的小正方形，在以此类推，无限重复的做出各种大小不一的正方形，就形成了茂密的“毕达哥拉斯树”。

由于三个正方形的内部形成了一个等腰直角三角形，所以通过勾股定理可得，小正方形的边长是大正方形的√2/2，在通过对小正方形重复上述过程，无限重复下去。如果假设其中的大正方形边长为1，在增加到第n 次时，会增加2n个小正方形，而每个小正方形的边长就是√2/2，则每一次增加的面积就是2n×(½√2)=1。

毕达哥拉斯树是无限的吗?

理论上来看，毕达哥拉斯树是可以无限重复的，因为将上诉的公式中的n设为无限次后，毕达哥拉斯树的面积就会趋于无限大。勾股树的面积也会更加茂密，但是在现实中并非如此。

因为当n大于5时，所有产生的小正方体互相重叠，所以毕达哥拉斯树的面积其实是有限的。因此毕达哥拉斯树其实只能生长在一个6×4的方格中里，当然具体的值不太容易求出。

毕达哥拉斯树的变种

最初的毕达哥拉斯树中的大正方形和小正方形夹角是不等的，所以有一种毕达哥拉斯树的变种就是改变夹角，当最开始的大正方形和小正方形之间的夹角变为60度时，中间的三角形就会变成等边三角形，这样每一个正方形的边长都是相等的。

但是这种变种也和正常的毕达哥拉斯树一样，是有限的，达到第四步的时候就会发生重叠，最后就会形成一个大六边形，里面全是边长相等的正方形。

结语：数学中还有不少有趣的现象，除了毕达哥拉斯树，还有结果永远是123的123黑洞，以及世界上最神奇的数字142857，都是数学上的智慧结晶。