世界十大数学难题 哥德巴赫、霍奇猜想等，你想试试吗

提到数学总是让小编默默吞下心头一口老血，当年，想当年，卒。关于数学不好是什么感受，有一句话概括的最为体贴，那就是从一本到三本的感觉，关于下面的内容大家感受一下，世界十大数学难题——

世界十大数学难题

一、P(多项式时间)问题对NP(非确定多项式时间)问题

二、霍奇猜想

三、庞加莱猜想

四、黎曼假设

五、杨-米尔斯存在性和质量缺口

六、纳维叶-斯托克斯方程的存在性与光滑性

七、贝赫和斯维讷通-戴尔猜想

八、费尔马大定理

九、四色问题

十、哥德巴赫猜想

一、P(多项式时间)问题对NP(非确定多项式时间)问题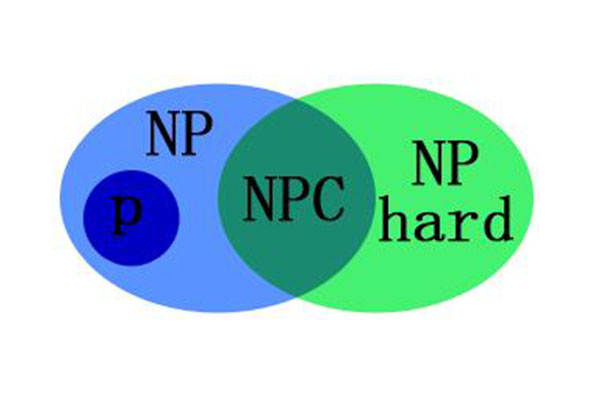

我不知道该怎么描述这个问题，但是他的原话大概是这样的：生成问题的一个解通常比验证一个给定的解时间花费要多得多。如果数13717421可以写成两个较小的数的乘积，你可能不知道是否应该相信他，但是如果他告诉你它可以因式分解为3607乘上3803，那么你就可以用一个袖珍计算器容易验证这是对的。

二、霍奇猜想

二十世纪的数学家们发现了研究复杂对象的形状的强有力的办法。霍奇猜想断言，对于所谓射影代数簇这种特别完美的空间类型来说，称作霍奇闭链的部件实际上是称作代数闭链的几何部件的(有理线性)组合。

三、庞加莱猜想

如果我们伸缩围绕一个苹果表面的橡皮带，那么我们可以既不扯断它，也不让它离开表面，使它慢慢移动收缩为一个点。另一方面，如果我们想象同样的橡皮带以适当的方向被伸缩在一个轮胎面上，那么不扯断橡皮带或者轮胎面，是没有办法把它收缩到一点的。我们说，苹果表面是“单连通的”，而轮胎面不是。数学界最终确认佩雷尔曼的证明解决了庞加莱猜想。

四、黎曼假设

素数的频率紧密相关于一个精心构造的所谓黎曼蔡塔函数z(s$的性态。著名的黎曼假设断言，方程z(s)=0的所有有意义的解都在一条直线上。这点已经对于开始的1,500,000,000个解验证过。证明它对于每一个有意义的解都成立将为围绕素数分布的许多奥秘带来光明。

五、杨-米尔斯存在性和质量缺口

杨振宁和米尔斯发现，量子物理揭示了在基本粒子物理与几何对象的数学之间的令人注目的关系。基于杨-米尔斯方程的预言已经在如下的全世界范围内的实验室中所履行的高能实验中得到证实：布罗克哈文、斯坦福、欧洲粒子物理研究所和筑波。在这一问题上的进展需要在物理上和数学上两方面引进根本上的新观念。

六、纳维叶-斯托克斯方程的存在性与光滑性

数学家和物理学家深信，无论是微风还是湍流，都可以通过理解纳维叶-斯托克斯方程的解，来对它们进行解释和预言，预言风的走向和水流的流向，就像一个大自然的指挥家。

七、贝赫和斯维讷通-戴尔猜想

当解是一个阿贝尔簇的点时，贝赫和斯维讷通-戴尔猜想认为，有理点的群的大小与一个有关的蔡塔函数z(s)在点s=1附近的性态。特别是，这个有趣的猜想认为，如果z(1)等于0,那么存在无限多个有理点(解)，相反，如果z(1)不等于0,那么只存在有限多个这样的点。

八、费尔马大定理

费尔马大定理起源于三百多年前，挑战了人类3个世纪，终于在1994年被安德鲁·怀尔斯攻克。具体内容被记述在古希腊的丢番图写过一本著名的“算术”中。

九、四色问题

四色问题的内容是：“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。”用数学语言表示，即“将平面任意地细分为不相重叠的区域，每一个区域总可以用1，2，3，4这四个数字之一来标记，而不会使相邻的两个区域得到相同的数字。”好了我晕了。

十、哥德巴赫猜想

猜想内容为：一是任何不小于6的偶数，都是两个奇质数之和;二是任何不小于9的奇数，都是三个奇质数之和。你看自己看吧，小编看完已经困的不行了。